2022)¶

Announcements

Last time we covered:

Tidy data (wide / long format)

Today’s agenda:

Data transformations

Part 1: logarithmic transformations

Part 2: z-scoring

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

Part 1: log transformations¶

Problem: highly skewed data¶

To get a sense of when we may need to transform our data, let’s take a look at our gapminder dataset once again:

gap = pd.read_csv("https://raw.githubusercontent.com/UCSD-CSS-002/ucsd-css-002.github.io/master/datasets/gapminder.csv")

gap

	Unnamed: 0	country	continent	year	lifeExp	pop	gdpPercap
0	1	Afghanistan	Asia	1952	28.801	8425333	779.445314
1	2	Afghanistan	Asia	1957	30.332	9240934	820.853030
2	3	Afghanistan	Asia	1962	31.997	10267083	853.100710
3	4	Afghanistan	Asia	1967	34.020	11537966	836.197138
4	5	Afghanistan	Asia	1972	36.088	13079460	739.981106
...	...	...	...	...	...	...	...
1699	1700	Zimbabwe	Africa	1987	62.351	9216418	706.157306
1700	1701	Zimbabwe	Africa	1992	60.377	10704340	693.420786
1701	1702	Zimbabwe	Africa	1997	46.809	11404948	792.449960
1702	1703	Zimbabwe	Africa	2002	39.989	11926563	672.038623
1703	1704	Zimbabwe	Africa	2007	43.487	12311143	469.709298

1704 rows × 7 columns

Below we plot the distribution of population across the countries in this dataset for the most recent year available.

What does it look like?

g = sns.histplot(
    data = gap[gap["year"] == 2007],
    x = "pop",
    bins = 60 # even with more bins the distribution is similar
)
g.set_xlabel("Population (billions)")
g.set_title("Population by country, 2007")

Text(0.5, 1.0, 'Population by country, 2007')

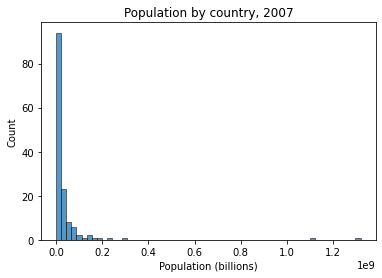
# How skewed is the data above?

gap["pop"][gap["year"] == 2007].mean() # ~44M
gap["pop"][gap["year"] == 2007].median() # ~10.5M

# ...big difference

10517531.0

Why this is a problem?

Most standard statistics assumes that the variables being predicted or serving as predictors are (roughly) normally distributed. Our population data above clearly isn’t!

How common is this?

The pattern above isn’t unique to population. Many other common variables tend to have similarly shaped distributions.

Can you think of some others? (hint: remember Zipf’s Law back in pset 1?)

Solution: with skewed data, use log transform!¶

What do we mean by log transforming?

We want to convert our population data to a logarithmic scale rather than a linear scale.

We’ll illustrate this difference below.

# Our original graph used bins scaled at a linear interval. We're printing them below. 

_ = sns.histplot(
    data = gap[gap["year"] == 2007],
    x = "pop",
    bins = 20
)

# Here's our original histogram bins: note how they increase by a fixed amount
print("Histogram bins: {}".format([str(elem) for elem in plt.xticks()[0]]))

# Can print each element minus the previous elemnt to show this
# [plt.xticks()[0][i+1] - plt.xticks()[0][i] for i in range(len(plt.xticks()[0])-1)]

Histogram bins: ['-200000000.0', '0.0', '200000000.0', '400000000.0', '600000000.0', '800000000.0', '1000000000.0', '1200000000.0', '1400000000.0']

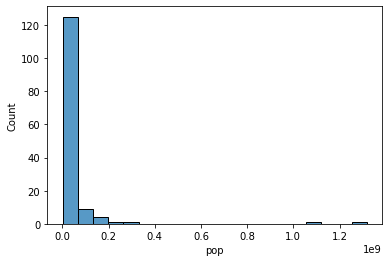
# Step 1: let's generate logarithmic scaled bins instead of the above.


# Instead of increasing by a fixed amount (200k), they will increase by a fixed *multiple* (10) from 100k to 1B
# Use `np.logspace` for this
log_bins = np.logspace(base = 10, # specify the base (10 is default)
                       start = 5, # specify the start, which is base**start (in this case 10e5)
                       stop = 9, # specify the end, which is base**end (in this case 10e9)
                       num = 10) # specify the number of bins

[str(elem) for elem in log_bins]

# These don't increase by a fixed amount
# Can print each element minus the previous element as we did above to show this

# [log_bins[i+1] - log_bins[i] for i in range(len(log_bins)-1)]

# Instead, they increase by a fixed *multiple*
# Can print each element in log_bins *divided by* the previous element to show this

# [log_bins[i+1] / log_bins[i] for i in range(len(log_bins)-1)]

['100000.0',
 '278255.94022071257',
 '774263.6826811278',
 '2154434.6900318824',
 '5994842.503189409',
 '16681005.372000592',
 '46415888.33612773',
 '129154966.50148827',
 '359381366.3804626',
 '1000000000.0']

# Now, let's use these logarithmic intervals as the basis for our histogram bins

g = sns.histplot(
    data = gap[gap["year"] == 2007],
    x = "pop",
    bins = log_bins # This is the key change
)

# NOTE: we need to also specify that the x axis should be drawn on a logarithmic scale 
# (try graphing without this to see what happens!)
g.set_xscale('log')

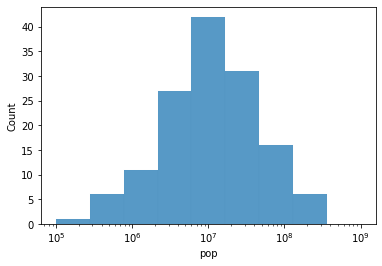
Our data looks normally distributed when we plot it on a log scale. Woo hoo!

But we haven’t changed the underlying data.

Let’s log transform the data itself so its (log) values are normally distributed.

# To do this, use np.log10 (np.log uses the *natural log*) 
gap['log_pop'] = np.log10(gap['pop'])

gap

	Unnamed: 0	country	continent	year	lifeExp	pop	gdpPercap	log_pop
0	1	Afghanistan	Asia	1952	28.801	8425333	779.445314	6.925587
1	2	Afghanistan	Asia	1957	30.332	9240934	820.853030	6.965716
2	3	Afghanistan	Asia	1962	31.997	10267083	853.100710	7.011447
3	4	Afghanistan	Asia	1967	34.020	11537966	836.197138	7.062129
4	5	Afghanistan	Asia	1972	36.088	13079460	739.981106	7.116590
...	...	...	...	...	...	...	...	...
1699	1700	Zimbabwe	Africa	1987	62.351	9216418	706.157306	6.964562
1700	1701	Zimbabwe	Africa	1992	60.377	10704340	693.420786	7.029560
1701	1702	Zimbabwe	Africa	1997	46.809	11404948	792.449960	7.057093
1702	1703	Zimbabwe	Africa	2002	39.989	11926563	672.038623	7.076515
1703	1704	Zimbabwe	Africa	2007	43.487	12311143	469.709298	7.090298

1704 rows × 8 columns

Now what? Let’s take a look at our log transformed population variable.

Is it normally distributed?

g = sns.histplot(data = gap[gap['year'] == 2007], x = 'log_pop')
g.set_xlabel("Log transformed population")

Text(0.5, 0, 'Log transformed population')

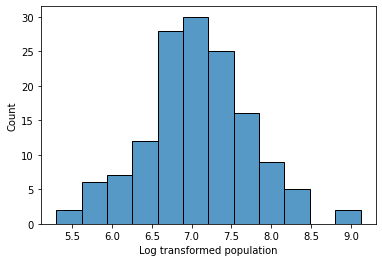
Log transformations: Summary¶

Statistics and modeling solutions often assume that the underlying variables are normally distributed
You can count on many variables in the world being roughly normally distributed (especially with large samples!)
But certain types of data are reliably not normally distributed (ex. income, wealth, population, number of Twitter followers, number of Spotify streams, …)
When your data looks like the examples above (rule of thumb: roughly exponentially distributed, or has very large right skew), it’s often the case that the logarithm of the data is normally distributed.
You can check whether this is true by plotting it on a log scale as we did above. If so, consider log transforming your data.

Note: using the log transformed values for a variable in statistics or regression changes how you interpret your results (for example, regression coefficients on a log-transformed variable X will reflect the impact of multiplicative changes to X on the output variable Y).

Part 2: z-scoring¶

Problem: comparing data from different distributions¶

To get a sense of when we may need to z-score our data, let’s take a look at our pokemon dataset once again:

pk = pd.read_csv("https://raw.githubusercontent.com/UCSD-CSS-002/ucsd-css-002.github.io/master/datasets/Pokemon.csv")

pk

	#	Name	Type 1	Type 2	Total	HP	Attack	Defense	Sp. Atk	Sp. Def	Speed	Generation	Legendary
0	1	Bulbasaur	Grass	Poison	318	45	49	49	65	65	45	1	False
1	2	Ivysaur	Grass	Poison	405	60	62	63	80	80	60	1	False
2	3	Venusaur	Grass	Poison	525	80	82	83	100	100	80	1	False
3	3	VenusaurMega Venusaur	Grass	Poison	625	80	100	123	122	120	80	1	False
4	4	Charmander	Fire	NaN	309	39	52	43	60	50	65	1	False
...	...	...	...	...	...	...	...	...	...	...	...	...	...
795	719	Diancie	Rock	Fairy	600	50	100	150	100	150	50	6	True
796	719	DiancieMega Diancie	Rock	Fairy	700	50	160	110	160	110	110	6	True
797	720	HoopaHoopa Confined	Psychic	Ghost	600	80	110	60	150	130	70	6	True
798	720	HoopaHoopa Unbound	Psychic	Dark	680	80	160	60	170	130	80	6	True
799	721	Volcanion	Fire	Water	600	80	110	120	130	90	70	6	True

800 rows × 13 columns

Let’s say we want to know whether each of our pokemon is going to be better off attacking opponents, or simply outlasting them.

The Attack variable indicates how strong they are at attacking, while HP indicates how long they can withstand attacks.

How would we evaluate which of these is stronger for each pokemon?

Strategy 1: look at which variable is larger

# "attacker" variable says whether a given pokemon has higher attack value than HP
pk['attacker'] = pk['Attack'] > pk['HP']

pk

	#	Name	Type 1	Type 2	Total	HP	Attack	Defense	Sp. Atk	Sp. Def	Speed	Generation	Legendary	attacker
0	1	Bulbasaur	Grass	Poison	318	45	49	49	65	65	45	1	False	True
1	2	Ivysaur	Grass	Poison	405	60	62	63	80	80	60	1	False	True
2	3	Venusaur	Grass	Poison	525	80	82	83	100	100	80	1	False	True
3	3	VenusaurMega Venusaur	Grass	Poison	625	80	100	123	122	120	80	1	False	True
4	4	Charmander	Fire	NaN	309	39	52	43	60	50	65	1	False	True
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
795	719	Diancie	Rock	Fairy	600	50	100	150	100	150	50	6	True	True
796	719	DiancieMega Diancie	Rock	Fairy	700	50	160	110	160	110	110	6	True	True
797	720	HoopaHoopa Confined	Psychic	Ghost	600	80	110	60	150	130	70	6	True	True
798	720	HoopaHoopa Unbound	Psychic	Dark	680	80	160	60	170	130	80	6	True	True
799	721	Volcanion	Fire	Water	600	80	110	120	130	90	70	6	True	True

800 rows × 14 columns

# We can plot this variable across our generations
sns.countplot(data = pk,
              x = 'Generation',
              hue = 'attacker'
             )

<AxesSubplot:xlabel='Generation', ylabel='count'>

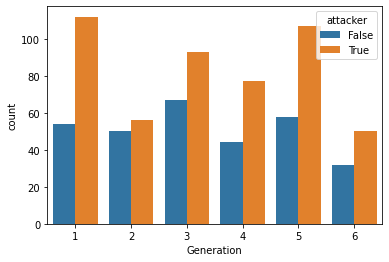
However, there’s one challenge with this strategy.

If many pokemon have higher Attack than HP values, we can’t always tell whether a pokemon has a greater advantage when attacking or withstanding an opponent by just looking at which value is higher.

To see this, take a look at the distribution of HP and Attack variables below.

# For the graph below, it's easiest to switch to tidy data!
pk_tidy = pk.melt(
    id_vars = ["#", "Name", "Type 1", "Type 2", "Generation", "Legendary", "attacker"]
)
pk_tidy


sns.histplot(
    data = pk_tidy[pk_tidy['variable'].isin(["HP", "Attack"])],
    x = "value",
    hue = "variable",
    kde = True,
    bins = 15
)

<AxesSubplot:xlabel='value', ylabel='Count'>

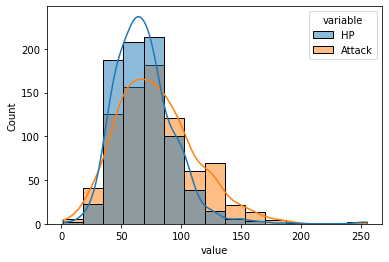
In the graph above, the Attack distribution is shifted right and seems more spread out than the HP distribution, so most pokemon will likely have higher Attack points.

What we really want to know might be something like: relative to the competition, does each pokemon have a more impressive Attack or HP value?

Solution: when comparing across (normal) distributions, try z-scores!¶

What is a z-score?

A z-score for a given observation \(x\) is the number of standard deviations away from the mean it is.

\(Z = \dfrac{x - \mu}{\sigma}\)

# Let's pre-compute the mean and standard deviation of each distribution in our data (Attack and HP)

mean_attack = pk['Attack'].mean() # 79
mean_hp = pk['HP'].mean() # 69

sd_attack = pk['Attack'].std() # 32.5
sd_hp = pk['HP'].std() # 25.5

# Note that these are fairly different in roughly the way we described above.

# Now, let's evaluate the z score for each pokemon's Attack and HP values

pk['attack_z'] = (pk['Attack'] - mean_attack) / sd_attack
pk['hp_z'] = (pk['HP'] - mean_hp) / sd_hp

pk

	#	Name	Type 1	Type 2	Total	HP	Attack	Defense	Sp. Atk	Sp. Def	Speed	Generation	Legendary	attacker	attack_z	hp_z
0	1	Bulbasaur	Grass	Poison	318	45	49	49	65	65	45	1	False	True	-0.924328	-0.950032
1	2	Ivysaur	Grass	Poison	405	60	62	63	80	80	60	1	False	True	-0.523803	-0.362595
2	3	Venusaur	Grass	Poison	525	80	82	83	100	100	80	1	False	True	0.092390	0.420654
3	3	VenusaurMega Venusaur	Grass	Poison	625	80	100	123	122	120	80	1	False	True	0.646964	0.420654
4	4	Charmander	Fire	NaN	309	39	52	43	60	50	65	1	False	True	-0.831899	-1.185007
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
795	719	Diancie	Rock	Fairy	600	50	100	150	100	150	50	6	True	True	0.646964	-0.754220
796	719	DiancieMega Diancie	Rock	Fairy	700	50	160	110	160	110	110	6	True	True	2.495543	-0.754220
797	720	HoopaHoopa Confined	Psychic	Ghost	600	80	110	60	150	130	70	6	True	True	0.955061	0.420654
798	720	HoopaHoopa Unbound	Psychic	Dark	680	80	160	60	170	130	80	6	True	True	2.495543	0.420654
799	721	Volcanion	Fire	Water	600	80	110	120	130	90	70	6	True	True	0.955061	0.420654

800 rows × 16 columns

What do z-score distributions look like?

sns.kdeplot(data = pk, x = 'attack_z', color = 'red', alpha = 0.5)
sns.kdeplot(data = pk, x = 'hp_z', color = 'green', alpha = 0.5)

plt.xlabel("Z score")

Text(0.5, 0, 'Z score')

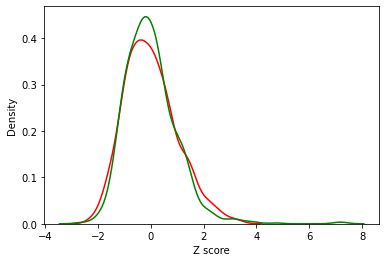
These are much more comparable!

Now, we can ask which pokemon have a higher z-scored Attack relative to their z-scored HP

pk['z_attacker'] = pk['attack_z'] > pk['hp_z']

pk

	#	Name	Type 1	Type 2	Total	HP	Attack	Defense	Sp. Atk	Sp. Def	Speed	Generation	Legendary	attacker	attack_z	hp_z	z_attacker
0	1	Bulbasaur	Grass	Poison	318	45	49	49	65	65	45	1	False	True	-0.924328	-0.950032	True
1	2	Ivysaur	Grass	Poison	405	60	62	63	80	80	60	1	False	True	-0.523803	-0.362595	False
2	3	Venusaur	Grass	Poison	525	80	82	83	100	100	80	1	False	True	0.092390	0.420654	False
3	3	VenusaurMega Venusaur	Grass	Poison	625	80	100	123	122	120	80	1	False	True	0.646964	0.420654	True
4	4	Charmander	Fire	NaN	309	39	52	43	60	50	65	1	False	True	-0.831899	-1.185007	True
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
795	719	Diancie	Rock	Fairy	600	50	100	150	100	150	50	6	True	True	0.646964	-0.754220	True
796	719	DiancieMega Diancie	Rock	Fairy	700	50	160	110	160	110	110	6	True	True	2.495543	-0.754220	True
797	720	HoopaHoopa Confined	Psychic	Ghost	600	80	110	60	150	130	70	6	True	True	0.955061	0.420654	True
798	720	HoopaHoopa Unbound	Psychic	Dark	680	80	160	60	170	130	80	6	True	True	2.495543	0.420654	True
799	721	Volcanion	Fire	Water	600	80	110	120	130	90	70	6	True	True	0.955061	0.420654	True

800 rows × 17 columns

# We can plot this variable across our generations
sns.countplot(data = pk,
              x = 'Generation',
              hue = 'z_attacker'
             )

# Note it's a little less dramatic than our previous plot!

<AxesSubplot:xlabel='Generation', ylabel='count'>

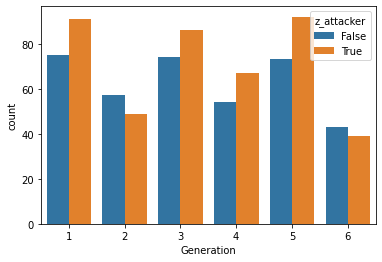
This plot provides a little more balanced picture than our previous one.

We can also use the z-scores to compare each pokemon’s Attack and HP in a more fine-grained way:

# Let's see which pokemon have the largest difference (in standard deviation units) between their `Attack` and `HP`
pk['attack_diff_normalized'] = pk['attack_z'] - pk['hp_z']

pk.nlargest(10, 'attack_diff_normalized')

	#	Name	Type 1	Type 2	Total	HP	Attack	Defense	Sp. Atk	Sp. Def	Speed	Generation	Legendary	attacker	attack_z	hp_z	z_attacker	attack_diff_normalized
429	386	DeoxysAttack Forme	Psychic	NaN	600	50	180	20	180	20	150	3	True	True	3.111736	-0.754220	True	3.865956
796	719	DiancieMega Diancie	Rock	Fairy	700	50	160	110	160	110	110	6	True	True	2.495543	-0.754220	True	3.249763
316	292	Shedinja	Bug	Ghost	236	1	90	45	30	30	40	3	False	True	0.338868	-2.673179	True	3.012047
428	386	DeoxysNormal Forme	Psychic	NaN	600	50	150	50	150	50	150	3	True	True	2.187446	-0.754220	True	2.941666
387	354	BanetteMega Banette	Ghost	NaN	555	64	165	75	93	83	75	3	False	True	2.649591	-0.205945	True	2.855537
232	214	HeracrossMega Heracross	Bug	Fighting	600	80	185	115	40	105	75	2	False	True	3.265784	0.420654	True	2.845131
527	475	GalladeMega Gallade	Psychic	Fighting	618	68	165	95	65	115	110	4	False	True	2.649591	-0.049296	True	2.698887
750	681	AegislashBlade Forme	Steel	Ghost	520	60	150	50	150	50	60	6	False	True	2.187446	-0.362595	True	2.550042
137	127	PinsirMega Pinsir	Bug	Flying	600	65	155	120	65	90	105	1	False	True	2.341495	-0.166783	True	2.508278
19	15	BeedrillMega Beedrill	Bug	Poison	495	65	150	40	15	80	145	1	False	True	2.187446	-0.166783	True	2.354230

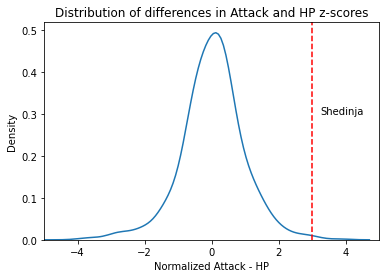
We can plot this distribution and use it to evaluate the relative strength of a given pokemon’s Attack

g = sns.kdeplot(data = pk,
            x = 'attack_diff_normalized'
           )


g.axvline(pk[pk['Name'] == 'Shedinja']['attack_diff_normalized'].iloc[0], # value to draw the line at
            color = 'red', # color
            ls = '--' # `linestyle`: '-', ':'
           )

g.text(3.25, 0.3, "Shedinja")

g.set_xlim(-5, 5)
g.set_title("Distribution of differences in Attack and HP z-scores")
g.set_xlabel("Normalized Attack - HP")

Text(0.5, 0, 'Normalized Attack - HP')

Z-scores: Summary¶

Sometimes for analysis purposes, you’ll want to compare variables that are measured on different scales or show differences in the underlying distribution (ex. how to compare SAT and ACT scores?)
To make these comparisons, it’s often easier to convert the data to a similar scale for comparison.
A z-score converts each data point to a number of standard deviations above or below the mean, which means you can more easily compare two scores that are otherwise very different or use these scores as the basis for regression or other analyses.

Lecture 11 (4/20/2022) Lecture 13 (4/25/22)

UCSD CSS 2