Contents

Lecture 16 (5/2/2022)

Announcements

Last time we covered:

  • Linear regression

    • Simple linear regression

    • Evaluating regression

    • Polynomial and multiple regression

Today’s agenda:

  • Multiple regression continued

  • Overfitting

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

Multiple Regression

Big idea: multiple predictors for \(y\)

In real-world scenarios, it’s common to explore the relationship between multiple predictor variables that all jointly impact the dependent variable.

For this, we need multiple regression.

Though the guiding principles are similar to simple regression, things can get much more complicated in multiple dimensions. Here, we’ll provide enough of an overview for you to be able to use multiple regression as part of your modeling toolbox.

Example: predicting life expectancy

Let’s start with a familiar example.

In Problem Set 3 and elsewhere, we’ve looked at the gapminder dataset, which explores the relationship between GDP, population, and life expectancy at the national level and over time.

Here, we’ll just look at these variables for the most recent year (2007).

gap = pd.read_csv("https://raw.githubusercontent.com/UCSD-CSS-002/ucsd-css-002.github.io/master/datasets/gapminder.csv")

# Let's keep just some of the variables (note for pset!)
# NOTE: we're also just restricting ourselves to 2007
gap_subset = gap.loc[gap['year'] == 2007, ('country', 'year', 'lifeExp', 'pop', 'gdpPercap')].reset_index(drop = True)

# Add log transformed population and income
gap_subset['logPop'] = np.log10(gap_subset['pop'])
gap_subset['logGdpPercap'] = np.log10(gap_subset['gdpPercap'])
gap_subset
country year lifeExp pop gdpPercap logPop logGdpPercap
0 Afghanistan 2007 43.828 31889923 974.580338 7.503653 2.988818
1 Albania 2007 76.423 3600523 5937.029526 6.556366 3.773569
2 Algeria 2007 72.301 33333216 6223.367465 7.522877 3.794025
3 Angola 2007 42.731 12420476 4797.231267 7.094138 3.680991
4 Argentina 2007 75.320 40301927 12779.379640 7.605326 4.106510
... ... ... ... ... ... ... ...
137 Vietnam 2007 74.249 85262356 2441.576404 7.930757 3.387670
138 West Bank and Gaza 2007 73.422 4018332 3025.349798 6.604046 3.480776
139 Yemen, Rep. 2007 62.698 22211743 2280.769906 7.346583 3.358081
140 Zambia 2007 42.384 11746035 1271.211593 7.069891 3.104218
141 Zimbabwe 2007 43.487 12311143 469.709298 7.090298 2.671829

142 rows × 7 columns

In Problem Set 3, you generated a graph that explored the relationship between income (GDP per-capita on \(x\)) and life expectancy (in years on \(y\)), alongside two additional predictors: region (color) and population (size).

gap

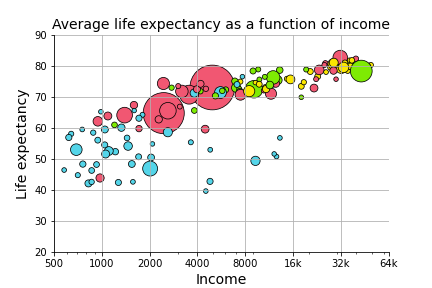
Here, we want to know formally what the relationship is between the three continuous variables (income, life expectancy, and population). In other words, can we predict life expectancy using both income and population better than we could only using one of those variables?

Let’s start by just examining each of the predictors in isolation to see if this is a plausible hypothesis.

g = sns.lmplot(data = gap_subset, 
                    x = "logGdpPercap", # x1 
                    y = "lifeExp"
                   )
plt.title("Life expectancy as a function of income")
plt.xlabel("Income (log GDP / capita)")
plt.ylabel("Life expectancy")
plt.show()

h = sns.lmplot(data = gap_subset, 
                    x = "logPop", # x2 
                    y = "lifeExp"
                   )
plt.title("Life expectancy as a function of population")
plt.xlabel("Population (log)")
plt.ylabel("Life expectancy")
plt.show()
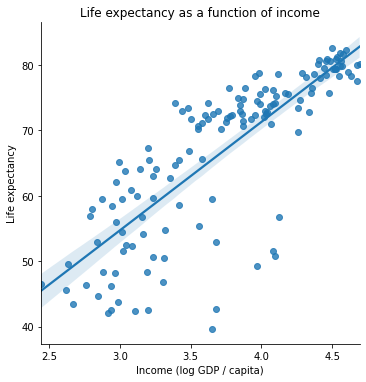
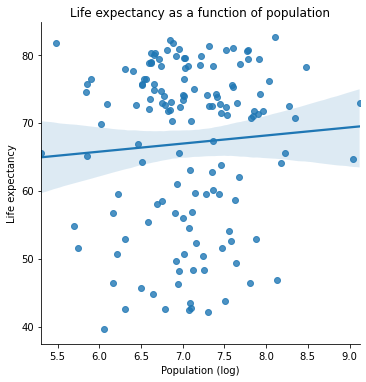
../../_images/Lecture_16-post_8_0.png ../../_images/Lecture_16-post_8_1.png

One of these variables has a strong positive relationship. The other one seems a bit less clear.

How can we think about exploring the role that both of them play together in predicting life expectancy?

Multiple regression: overview

Multiple regression is like linear regression except that we assume our dependent variable \(y_i\) is jointly predicted by multiple independent variables:

\(x_1\), \(x_2\), …, \(x_n\).

Simple linear regression generates a predicted \(\hat{y}_i\) from \(x_i\):

\(\hat{y}_i = \beta_0 + \beta_1 x_i + \epsilon_i\)

With multiple regression, we now extend this model to include multiple predictors for our data (\(x_{1i}\), \(x_{2i}\), …, \(x_{ni}\)):

\(\hat{y}_i = \beta_0 + \beta_1 x_{1i} + \beta_2 x_{2i} + \ ... \ + \beta_n x_{ni} + \epsilon_i \)

In most cases, multiple regression once again uses the same Ordinary Least Squares (OLS) parameter estimation as simple regression. However, interpreting the parameter estimates is a little less straightforward.

How would we interpret \(\beta_0 = 1\), \(\beta_1 = 2\), \(\beta_2 = 3\)?

(Think of a simple example. What variables would you want to use to predict somebody’s height as accurately as possible? Now imagine each of those variables is one of your \(x_{ji}\) variables.)

Multiple regression in python

The scikit-learn LinearRegression class is very easy to extend to multiple regression!

We’ll also demonstrate the statsmodels approach below for more robust statistical analysis.

# scikit learn approach
from sklearn.linear_model import LinearRegression

x_vals = np.array(gap_subset[['logGdpPercap', 'logPop']]) # Note: this double bracket syntax is important!
x_vals = x_vals.reshape(len(gap_subset), 2)
x_vals

y_vals = np.array(gap_subset['lifeExp'])
y_vals

mod = LinearRegression().fit(X = x_vals, y = y_vals)

mod.intercept_
mod.coef_

array([16.6811828 ,  1.86827925])

What do the coefficient estimates above suggest?

How should we interpret them?

# R^2 for our regression
mod.score(X = x_vals, y = y_vals)

0.6649393884784984

# What if we don't include the population predictor?
x_single = np.array(gap_subset['logGdpPercap']).reshape(len(gap_subset), 1)
x_single

mod_simple = LinearRegression().fit(X = x_single, y = y_vals)
mod_simple.score(X = x_single, y = y_vals)

# Doesn't seem like population helps much...

0.6544490472926064

The statsmodels approach gives us a bit more insight here.

# statsmodels approach
import statsmodels.formula.api as smf

multiple_reg = smf.ols('lifeExp ~ logGdpPercap + logPop', data = gap_subset).fit()

# View the results
multiple_reg.summary()

# Our population variable does have a significant positive slope, 
# but it's pretty small and the effect may be driven by outliers.
OLS Regression Results
Dep. Variable: lifeExp R-squared: 0.665
Model: OLS Adj. R-squared: 0.660
Method: Least Squares F-statistic: 137.9
Date: Wed, 25 May 2022 Prob (F-statistic): 9.91e-34
Time: 09:23:15 Log-Likelihood: -477.07
No. Observations: 142 AIC: 960.1
Df Residuals: 139 BIC: 969.0
Df Model: 2
Covariance Type: nonrobust
coef std err t P>|t| [0.025 0.975]
Intercept -8.6161 7.538 -1.143 0.255 -23.520 6.288
logGdpPercap 16.6812 1.008 16.555 0.000 14.689 18.673
logPop 1.8683 0.896 2.086 0.039 0.098 3.639
Omnibus: 34.155 Durbin-Watson: 2.170
Prob(Omnibus): 0.000 Jarque-Bera (JB): 54.987
Skew: -1.183 Prob(JB): 1.15e-12
Kurtosis: 4.923 Cond. No. 104.


Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

Regression: wrap-up

Regression is one of the most powerful tools in our data science / analysis toolkit.

However, it’s important to be familiar with the limitations in regression as well.

One class of these limitations is when the data violate the assumptions of linear regression. We’re not going to get into these issues in this class, but it’s good to be aware that not all data (even data that looks linear!) can be accurately described by linear regression. There are a number of tricks for diagnosing this, such as plotting your residuals (we may explore this on the problem set as a way to cover some of this material).

However, an important limitation that we will discuss now is when regression overfits the data. Avoiding overfitting is something that arises in just about any modeling context. It’s easiest to illustrate with regression, but the things we discuss here will be relevant throughout the remainder of the quarter.

Overfitting

What is it?

The basic principle behind overfitting is that when your modeling approach is sufficiently unconstrained, you can fit patterns in your data that do not generalize.

What does it mean for a model to be unconstrained? What does it mean for the model not to generalize?

…

How does this happen?

There are lots of ways this can arise (and what it looks like differs across modeling techniques).

Let’s look at a canonical example just to get an intuition. For models that we learn about throughout the rest of the quarter, it’s a useful exercise to think about what overfitting might look like.

Example

Let’s return to our gapminder dataset and the task of predicting life expectancy (\(y\)) based on income (\(x\)).

What kind of relationship do we think these variables have in the data below?

gap_subset


g = sns.scatterplot(data = gap_subset, 
                    x = "logGdpPercap", # x1 
                    y = "lifeExp",
                    color = "r",
                    alpha = 0.5
                   )
plt.title("Life expectancy as a function of income")
plt.xlabel("Income (log GDP / capita)")
plt.ylabel("Life expectancy")
plt.show()
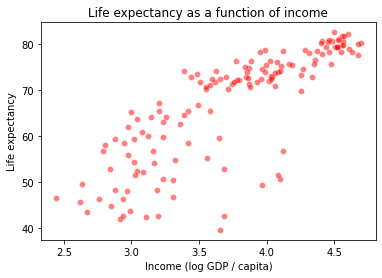
../../_images/Lecture_16-post_22_0.png

Let’s start with a simple linear regression:

# Estimate the model
x_vals = np.array(gap_subset['logGdpPercap']).reshape(len(gap_subset), 1)
y_vals = np.array(gap_subset['lifeExp'])
deg1_fits = LinearRegression().fit(X = x_vals, y = y_vals)

# Add predictions for this model to our dataframe
preds = gap_subset.loc[:, ("logGdpPercap", "lifeExp")].reset_index(drop = True)
simple_preds = deg1_fits.predict(X = x_vals)


preds['deg1_pred'] = simple_preds

preds
logGdpPercap lifeExp deg1_pred
0 2.988818 43.828 54.519342
1 3.773569 76.423 67.534497
2 3.794025 72.301 67.873765
3 3.680991 42.731 65.999076
4 4.106510 75.320 73.056337
... ... ... ...
137 3.387670 74.249 61.134339
138 3.480776 73.422 62.678496
139 3.358081 62.698 60.643606
140 3.104218 42.384 56.433262
141 2.671829 43.487 49.262068

142 rows × 3 columns

# Plot the fit

sns.scatterplot(data = preds, 
                x = "logGdpPercap",
                y = "lifeExp",
                color = "m",
                alpha = 0.5
               )
sns.lineplot(data = preds,
             x = "logGdpPercap",
             y = "deg1_pred"
            )


plt.title("Life expectancy as a function of income")
plt.xlabel("Income (log GDP / capita)")
plt.ylabel("Life expectancy")
plt.show()
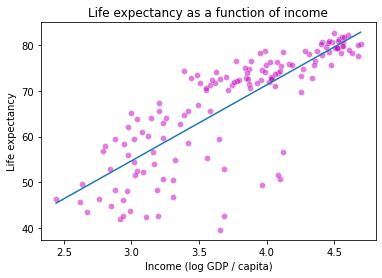
../../_images/Lecture_16-post_25_0.png

How did we do? Maybe this data is quadratic or cubic?

from sklearn.preprocessing import PolynomialFeatures

# Fit degree 2 polynomial regression
poly2 = PolynomialFeatures(degree = 2, include_bias = False)
x2_features = poly2.fit_transform(x_vals)
mod2 = LinearRegression().fit(x2_features, y_vals)

# Fit degree 3 polynomial regression
poly3 = PolynomialFeatures(degree = 3, include_bias = False)
x3_features = poly3.fit_transform(x_vals)
mod3 = LinearRegression().fit(x3_features, y_vals)

# Add these to our predictions
preds['deg2_pred'] = mod2.predict(X = x2_features)
preds['deg3_pred'] = mod3.predict(X = x3_features)
preds

# How do these predictions look at first glance? More accurate?
logGdpPercap lifeExp deg1_pred deg2_pred deg3_pred
0 2.988818 43.828 54.519342 54.128139 54.071604
1 3.773569 76.423 67.534497 68.392417 68.422855
2 3.794025 72.301 67.873765 68.722745 68.758756
3 3.680991 42.731 65.999076 66.871091 66.875117
4 4.106510 75.320 73.056337 73.506613 73.595809
... ... ... ... ... ...
137 3.387670 74.249 61.134339 61.765814 61.694179
138 3.480776 73.422 62.678496 63.433290 63.381871
139 3.358081 62.698 60.643606 61.226743 61.149956
140 3.104218 42.384 56.433262 56.420367 56.336913
141 2.671829 43.487 49.262068 47.486363 47.642830

142 rows × 5 columns

Let’s plot these lines and see how they look:

# First, let's make our data tidy for easier plotting
preds_long = preds.melt(
    id_vars = ["logGdpPercap", "lifeExp"],
    var_name = "degree",
    value_name = "prediction"
)

preds_long

# Now, let's take a look
sns.scatterplot(data = preds_long, 
                x = "logGdpPercap",
                y = "lifeExp",
                color = "m",
                alpha = 0.1
               )

sns.lineplot(
    data = preds_long,
    x = "logGdpPercap",
    y = "prediction",
    hue = "degree"
)

<AxesSubplot:xlabel='logGdpPercap', ylabel='lifeExp'>
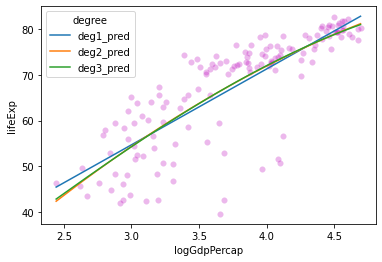
../../_images/Lecture_16-post_29_1.png

These lines look pretty similar. Do we see any change in \(R^2\) values for these models?

# Get R^2 for each model
mod1_rsq = deg1_fits.score(X = x_vals, y = y_vals)
mod2_rsq = mod2.score(X = x2_features, y = y_vals)
mod3_rsq = mod3.score(X = x3_features, y = y_vals)

print("Degree 1 R^2: {} \nDegree 2 R^2: {} \nDegree 3 R^2: {}".format(
    mod1_rsq, mod2_rsq, mod3_rsq
))

Degree 1 R^2: 0.6544490472926064 
Degree 2 R^2: 0.6588616234359694 
Degree 3 R^2: 0.6589091468875565

What does this tell us?

Probably don’t need 2nd or 3rd degree polynomials for this relationship.

What happens if we try to fit a much higher-order polynomial function to this data? Similar line or something else?

???

# Fit degree 10 polynomial regression
poly10 = PolynomialFeatures(degree = 10, include_bias = False)
x10_features = poly10.fit_transform(x_vals)
mod10 = LinearRegression().fit(x10_features, y_vals)

Let’s compare this one to our \(R^2\) values above:

# Calculate R^2 for our degree 10 polynomial
mod10_rsq = mod10.score(X = x10_features, y = y_vals)
mod10_rsq

0.6708222009621823

Improvement! Let’s keep going!

# Fit degree 25 polynomial regression
poly25 = PolynomialFeatures(degree = 25, include_bias = False)
x25_features = poly25.fit_transform(x_vals)
mod25 = LinearRegression().fit(x25_features, y_vals)

# Check R^2
mod25_rsq = mod25.score(X = x25_features, y = y_vals)
mod25_rsq

0.6716693321510845

Okay maybe things are slowing down…

Let’s plot our functions and see how they look.

# Add to predictions dataframe and re-format
preds['deg10_pred'] = mod10.predict(X = x10_features)
preds['deg25_pred'] = mod25.predict(X = x25_features)

preds_long = preds.melt(
    id_vars = ["logGdpPercap", "lifeExp"],
    var_name = "degree",
    value_name = "prediction"
)

preds_long

# Now, let's take a look
sns.scatterplot(data = preds_long, 
                x = "logGdpPercap",
                y = "lifeExp",
                color = "m",
                alpha = 0.1
               )

sns.lineplot(
    data = preds_long,
    x = "logGdpPercap",
    y = "prediction",
    hue = "degree"
)

<AxesSubplot:xlabel='logGdpPercap', ylabel='lifeExp'>
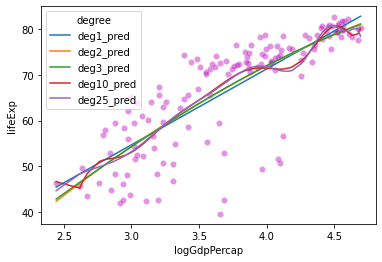
../../_images/Lecture_16-post_39_1.png

Hmmm….

sns.lineplot(
    data = preds,
    x = "logGdpPercap",
    y = "deg10_pred",
    color = "r"
)
plt.xlabel("Income")
plt.ylabel("Predicted life expectancy")
plt.show()

sns.lineplot(
    data = preds,
    x = "logGdpPercap",
    y = "deg25_pred",
    color = "b"
)
plt.xlabel("Income")
plt.ylabel("Predicted life expectancy")
plt.show()
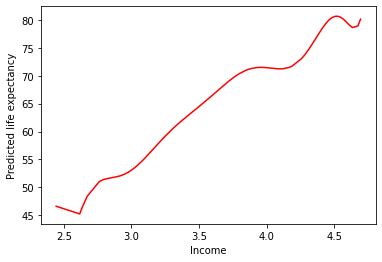
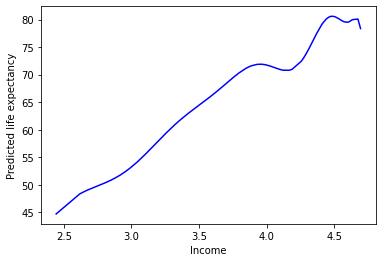
../../_images/Lecture_16-post_41_0.png ../../_images/Lecture_16-post_41_1.png

This doesn’t seem like it’s capturing the underlying process that generated our data…

spaghetti

Aside: overfitting is easiest to demonstrate with polynomial regression because it makes Least Squares Spaghetti. However, this problem can arise in almost any modeling context. Think about what this might look like with multiple regression.

Overfitting summary

The high-degree polynomials above are unconstrained, leading them to fit our data too well.

This creates worries that they won’t generalize.

But how do we test this?

Cross-validation: avoiding overfitting

There are many different techniques for cross-validation, one of which we discussed on Friday.

However, at their heart, all of them involve the same underlying principle: estimate your model parameters with only a subset (or repeated subsets) of your data, then evaluate your model on the remaining data to ensure generalizability.

This technique allows you to ensure that your model is a good fit, or do model comparison to choose among different candidate models (such as our polynomial models above).

Rather than go through all of the different ways of doing this, I’ll walk through a few of the more well known ones. This will give you a feel for how cross-validation works.

  1. Holdout cross-validation: this is the technique we reviewed on Friday

    • Split data into training and test data (e.g. 75-25 split)

    • Train model on training data only

    • Evaluate model on test data

  2. k-fold cross-validation: This is a more robust version of holdout cross-validation

    • Split data into k equal sized buckets (randomly!)

    • Choose one of the buckets to be test data and assign the rest to be training data

    • Perform holdout cross-validation with this data

    • Then, repeat the above for each of the other buckets and average your test results (e.g., MSE) over the multiple runs

  3. Monte-carlo cross-validation (repeated random subsampling): Similar to k-fold, but random

    • Split the data into training and test data randomly

    • Evaluate model on test data

    • Repeat this process many times

  4. Exhaustive cross-validation (various methods): The most common of these are leave-one-out or leave-p-out cross-validation

    • For every individual value in the data or set of \(p\) values, train the model on all remaining data then evalute the model using this individual or set of \(p\) values

    • Note: this is exhaustive because every data point or set of \(p\) data points is used in the test set, but is often computationally intractable!

  5. Other methods: specific to particular types of data (e.g., time series data, classification data)

For more info on this, you can check out this blog, or the wikipedia page devoted to this topic, or many others like it online!

Cross-Validation Summary

The techniques above are used with many if not all of the modeling techniques we’ll discuss this quarter.

From here on out, you should assume that some form of cross-validation is a required component of any model fitting process, much like looking at your data, cleaning it, and other core aspects of analysis.

Lecture 15 (4/29/2022) Lecture 17 (5/4/2022)