2022)¶

Announcements

Pset 4 will be released today, due next Friday 5/6

Last time we covered:

Evaluating regression: \(R^2\), out-of-sample prediction, parameter interpretation

Today’s agenda:

Polynomial regression, multiple regression

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

# Read in and prepare the data we were using last time
mpg = sns.load_dataset('mpg')
mpg_clean = mpg.dropna().reset_index(drop = True)

mpg_clean

	mpg	cylinders	displacement	horsepower	weight	acceleration	model_year	origin	name
0	18.0	8	307.0	130.0	3504	12.0	70	usa	chevrolet chevelle malibu
1	15.0	8	350.0	165.0	3693	11.5	70	usa	buick skylark 320
2	18.0	8	318.0	150.0	3436	11.0	70	usa	plymouth satellite
3	16.0	8	304.0	150.0	3433	12.0	70	usa	amc rebel sst
4	17.0	8	302.0	140.0	3449	10.5	70	usa	ford torino
...	...	...	...	...	...	...	...	...	...
387	27.0	4	140.0	86.0	2790	15.6	82	usa	ford mustang gl
388	44.0	4	97.0	52.0	2130	24.6	82	europe	vw pickup
389	32.0	4	135.0	84.0	2295	11.6	82	usa	dodge rampage
390	28.0	4	120.0	79.0	2625	18.6	82	usa	ford ranger
391	31.0	4	119.0	82.0	2720	19.4	82	usa	chevy s-10

392 rows × 9 columns

Review: Evaluating linear regression¶

In last lecture, we talked about three ways of checking that your regression fit the data well.

\(R^2\) coefficient of determination
Out of sample prediction accuracy
High confidence (and useful) parameter estimates

Let’s start by running through each of these in a little more detail since we didn’t get much time to discuss them.

\(R^2\), the coefficient of determination¶

determination

\( R^2 = 1 - \dfrac{RSS}{TSS} \)

\( RSS = \sum_{i=1}^{n}{(y_i - \hat{y_i})}^2 \)

\( TSS = \sum_{i=1}^{n}{(y_i - \bar{y})}^2 \)

\(R^2\) ranges between 0 and 1 and can be thought of as the percentage of variance in \(y\) that our model explains.

To understand how it works, remember that RSS is 0 when the regression perfectly predicts our data and RSS is equal to TSS when we just guess \(\bar{y}\) for every data point \(y_i\) (worst case for our regression).

# The scikit-learn LinearRegression class surfaces a function called `score` that computes R^2

from sklearn.linear_model import LinearRegression

# Format values
x_vals = np.array(mpg_clean['weight']).reshape(len(mpg_clean['weight']), 1)
y_vals = np.array(mpg_clean['horsepower'])

# Fit regression
mod = LinearRegression().fit(X = x_vals, y = y_vals)

rsq_mod = mod.score(X = x_vals, y = y_vals) # R^2 value
rsq_mod

0.74742549968982

Last time, we showed how to calculate the \(R^2\) value by hand using the LinearRegression predict function.

If you’re feeling hazy on \(R^2\), I recommend going back to the code from that lecture and going through the part where we calculate \(R^2\).

Out of sample prediction¶

train

Motivation

If our model is the right fit to our data, it should predict other data from the same underlying distribution or generative process pretty well.

How to check this

There are a lot of ways to test out of sample data which we’ll get into in more detail on Monday, but the high-level approach is almost always:

Randomly select a subset of your original data (20-25%) and set it aside as test data. The remaining data is your training data.
Fit your model to the training data only.
See how well your fitted model predicts the test data. Compare it to the predictions on the training data with something like Mean Squared Error (MSE).
Often, repeat steps 1-3 in various ways (more on that later).

Comparing train and test performance

Step 3 above is critical. One common approach is to use Mean Squared Error (MSE):

\( MSE = \dfrac{1}{n - 2} \sum_{i=1}^{n}{(y_i - \hat{y_i})}^2 = \dfrac{1}{n - 2} \sum_{i=1}^{n}{\epsilon_i}^2 \)

This tells you, on average, how close your model was to the true value across all the data points (the \(n-2\) is specific to linear regression where we have two parameters, \(\beta_0\) and \(\beta_1\), so \(n-2\) is our degrees of freedom).

from sklearn.model_selection import train_test_split # Use the sklearn `train_test_split` to make this easy
from sklearn.metrics import mean_squared_error # Use the sklearn `mean_squared_error` for quick MSE calculation

# Randomly sample 25% of our data points to be test data
xtrain, xtest, ytrain, ytest = train_test_split(x_vals, 
                                                y_vals, 
                                                test_size = 0.25
                                               )
# Fit the model on the training data
mod_tr = LinearRegression().fit(X = xtrain, y = ytrain)

# Generate model predictions for the test data
mod_preds_test = mod_tr.predict(X = xtest)

# Compare MSE for the model predictions on train and test data
mod_preds_train = mod_tr.predict(X = xtrain)

mse_train = mean_squared_error(y_true = ytrain, y_pred = mod_preds_train)
mse_train # Note this divides by n rather than n-2 but that's not super important for our purposes

mse_test = mean_squared_error(y_true = ytest, y_pred = mod_preds_test)
mse_test

print("Training MSE: {} \nTest MSE: {}".format(mse_train, mse_test))

Training MSE: 395.0045746066959 
Test MSE: 308.06816826493235

Just for fun, try running the code above several times and look at how different the values are.

More on this next week…

Parameter estimates¶

right

The criteria above are mostly concerned with whether we’re doing a good job predicting our \(y\) values with this model.

In many cases, part of what we’re concerned with isn’t just how well we predict our data, but what kind of relationship our model estimates between \(x\) and \(y\).

How large or small is the slope?
How confident are we in the estimate?

To assess this, we typically compute confidence bounds on the parameter estimates (95% confidence interval or standard error) and compare them to a null value of 0 using \(t\) tests.

Linear regression parameter estimates are most useful when they are high confidence and significantly different from 0.

The sklearn LinearRegression class doesn’t include functions for this sort of analysis, but other tools like the statsmodels regression class do.

import statsmodels.formula.api as smf

# Fit the model
results = smf.ols('horsepower ~ weight', data = mpg_clean).fit()

# View the results
results.summary()

OLS Regression Results
Dep. Variable:	horsepower	R-squared:	0.747
Model:	OLS	Adj. R-squared:	0.747
Method:	Least Squares	F-statistic:	1154.
Date:	Wed, 25 May 2022	Prob (F-statistic):	1.36e-118
Time:	09:23:01	Log-Likelihood:	-1717.0
No. Observations:	392	AIC:	3438.
Df Residuals:	390	BIC:	3446.
Df Model:	1
Covariance Type:	nonrobust

	coef	std err	t	P>\|t\|	[0.025	0.975]
Intercept	-12.1835	3.570	-3.412	0.001	-19.203	-5.164
weight	0.0392	0.001	33.972	0.000	0.037	0.041

Omnibus:	83.255	Durbin-Watson:	1.014
Prob(Omnibus):	0.000	Jarque-Bera (JB):	312.937
Skew:	0.892	Prob(JB):	1.11e-68
Kurtosis:	6.997	Cond. No.	1.13e+04

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 1.13e+04. This might indicate that there are
strong multicollinearity or other numerical problems.

Problems with simple linear regression¶

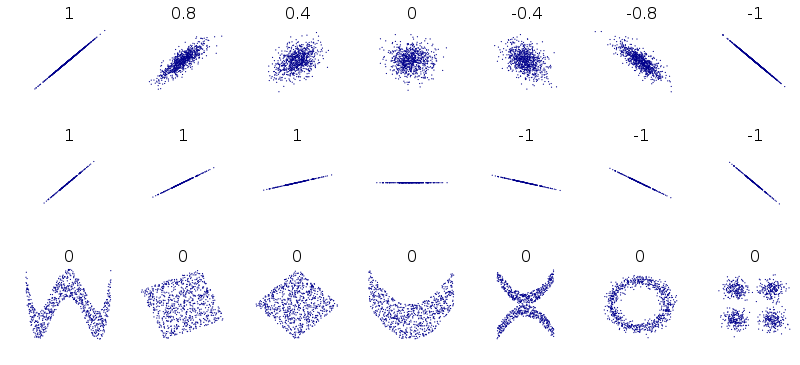corr_ex Disclaimer: this figure (from wikipedia) shows correlation values associated with these datasets, but the limitations of correlation in capturing these patterns holds for linear regression as well.

Polynomial regression: non-linear relationship between \(x\) and \(y\)¶

Non-linear data can take all kinds of forms, though there are probably a few that are most common.

Let’s take a look at a simple example from our cars dataset:

sns.lmplot(data = mpg_clean, x = "horsepower", y = "mpg")

<seaborn.axisgrid.FacetGrid at 0x7fce6b778b80>

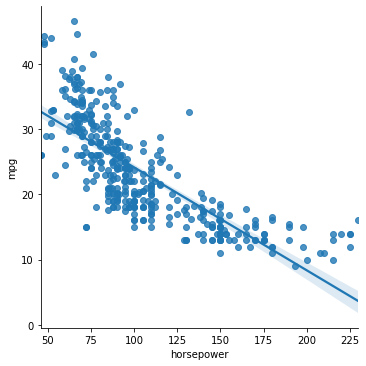
Does this data have a linear relationship between \(x\) and \(y\)? Seems like it might be more complicated.

Enter: polynomial regression!

Polynomial regression: overview¶

Polynomial regression is just like linear regression except that instead of fitting a linear function to the data, we fit higher degree polynomials.

Previously, our simple linear regression model assumed that our data \((x_i, y_i)\) could be described as:

\(y_i = \beta_0 + \beta_1 x_i + \epsilon_i\)

The OLS process estimates values for \(\beta_0\) and \(\beta_1\) that correspond to a straight line that minimizes \(\epsilon_i\).

With polynomial regression, we extend this basic model to include functions of the form:

\(y_i = \beta_0 + \beta_1 x_i + \beta_2 x_i^2 + \epsilon_i\) for degree 2 polynomial regression,

\(y_i = \beta_0 + \beta_1 x_i + \beta_2 x_i^2 + \beta_3 x_i^3 + \epsilon_i\) for degree 3 polynomial regression,

\(y_i = \beta_0 + \beta_1 x_i + \beta_2 x_i^2 + \beta_3 x_i^3 + \ ... \ + \beta_n x_i^n + \epsilon_i\) for degree n polynomial regression.

Even though this seems much more complex, polynomial regression uses the same Ordinary Least Squares (OLS) parameter estimation as simple regression. You can think of simple linear regression as a special case of polynomial regression.

This gives us immense flexibility to fit more complex functions to our data. Some of the data illustrated at the top of this section can only be modeled using more complex polynomials (see example below as well).

CAUTION: most of the time you don’t need polynomials to capture your data. Bad things happen when you use them for data that doesn’t have an underlying non-linear structure. More on this on Monday.

poly

Polynomial regression in python¶

We can use the numpy polyfit library to fit 2nd and 3rd order polynomials to this data (Note: this is probably the simplest method, but there’s code to use the familiar scikit learn approach as well below).

# We can fit higher order polynomial functions to our data rather than just a linear function
deg1_fits = np.polyfit(mpg_clean.horsepower, mpg_clean.mpg, 1)
deg2_fits = np.polyfit(mpg_clean.horsepower, mpg_clean.mpg, 2)
deg3_fits = np.polyfit(mpg_clean.horsepower, mpg_clean.mpg, 3)

p1 = np.poly1d(deg1_fits)
p2 = np.poly1d(deg2_fits)
p3 = np.poly1d(deg3_fits)

# What do the functions fitted above predict for our data?

preds = mpg_clean.loc[:, ('horsepower', 'mpg')]

preds['deg1_pred'] = p1(preds['horsepower'])
preds['deg2_pred'] = p2(preds['horsepower'])
preds['deg3_pred'] = p3(preds['horsepower'])

preds

preds_long = preds.melt(
    id_vars = ['horsepower', 'mpg']
)
preds

	horsepower	mpg	deg1_pred	deg2_pred	deg3_pred
0	130.0	18.0	19.416046	17.091508	17.153421
1	165.0	15.0	13.891480	13.480156	13.782683
2	150.0	18.0	16.259151	14.658717	14.890157
3	150.0	16.0	16.259151	14.658717	14.890157
4	140.0	17.0	17.837598	15.752059	15.904046
...	...	...	...	...	...
387	86.0	27.0	26.361214	25.908837	25.774667
388	52.0	44.0	31.727935	35.985609	36.424392
389	84.0	32.0	26.676903	26.422834	26.298564
390	79.0	28.0	27.466127	27.750895	27.662364
391	82.0	31.0	26.992593	26.946675	26.834765

392 rows × 5 columns

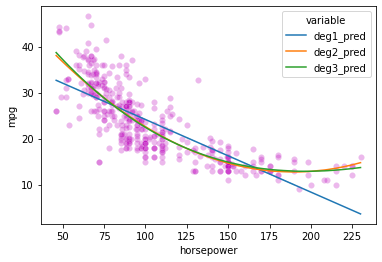
# First, our original data
sns.scatterplot(data = preds_long,
                x = 'horsepower',
                y = 'mpg',
                color = 'm',
                alpha = 0.1
               )

# Now add in our lines
sns.lineplot(data = preds_long,
             x = 'horsepower',
             y = 'value',
             hue = 'variable'
            )

<AxesSubplot:xlabel='horsepower', ylabel='mpg'>

Here’s the solution using scikit learn; it’s a bit more complicated, though it does let you keep using the LinearRegression class

from sklearn.preprocessing import PolynomialFeatures

x_vals = np.array(mpg_clean['horsepower']).reshape(len(mpg_clean['horsepower']), 1)
y_vals = np.array(mpg_clean['mpg'])
preds = mpg_clean.loc[:, ('horsepower', 'mpg')]

# Simple linear model
mod1 = LinearRegression().fit(x_vals, y_vals)

# 2nd order polynomial
poly2 = PolynomialFeatures(degree = 2, include_bias = False)
x2_features = poly2.fit_transform(x_vals)
mod2 = LinearRegression().fit(x2_features, y_vals)


# 3rd order polynomial
poly3 = PolynomialFeatures(degree = 3, include_bias = False)
x3_features = poly3.fit_transform(x_vals)
mod3 = LinearRegression().fit(x3_features, y_vals)


mod2.coef_
# mod3.coef_

array([-0.46618963,  0.00123054])

# Add predictions for each model so we can view how it does
preds['deg1_pred'] = mod1.predict(x_vals)
preds['deg2_pred'] = mod2.predict(x2_features)
preds['deg3_pred'] = mod3.predict(x3_features)

preds

	horsepower	mpg	deg1_pred	deg2_pred	deg3_pred
0	130.0	18.0	19.416046	17.091508	17.153421
1	165.0	15.0	13.891480	13.480156	13.782683
2	150.0	18.0	16.259151	14.658717	14.890157
3	150.0	16.0	16.259151	14.658717	14.890157
4	140.0	17.0	17.837598	15.752059	15.904046
...	...	...	...	...	...
387	86.0	27.0	26.361214	25.908837	25.774667
388	52.0	44.0	31.727935	35.985609	36.424392
389	84.0	32.0	26.676903	26.422834	26.298564
390	79.0	28.0	27.466127	27.750895	27.662364
391	82.0	31.0	26.992593	26.946675	26.834765

392 rows × 5 columns

preds_long = preds.melt(
    id_vars = ['horsepower', 'mpg']
)
preds

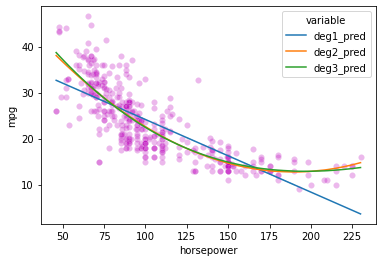
# First, our original data
sns.scatterplot(data = preds_long,
                x = 'horsepower',
                y = 'mpg',
                color = 'm',
                alpha = 0.1
               )

# Now add in our lines
sns.lineplot(data = preds_long,
             x = 'horsepower',
             y = 'value',
             hue = 'variable'
            )

<AxesSubplot:xlabel='horsepower', ylabel='mpg'>

# Let's check the R^2 values for these models to see what kind of improvement we get
# (more on this next week)

Multiple regression: multiple predictors for \(y\)¶

Another basic scenario that arises when predicting a continuous variable (probably more commonly than polynomial regression) is having multiple predictors.

Let’s take a look at an intuitive example:

gap = pd.read_csv("https://raw.githubusercontent.com/UCSD-CSS-002/ucsd-css-002.github.io/master/datasets/gapminder.csv")

# Let's keep just some of the variables (note for pset!)
gap_subset = gap.loc[gap['year'] == 2007, ('country', 'year', 'lifeExp', 'pop', 'gdpPercap')]

# Add log population
gap_subset['logPop'] = np.log10(gap_subset['pop'])
gap_subset['logGdpPercap'] = np.log10(gap_subset['gdpPercap'])
gap_subset

	country	year	lifeExp	pop	gdpPercap	logPop	logGdpPercap
11	Afghanistan	2007	43.828	31889923	974.580338	7.503653	2.988818
23	Albania	2007	76.423	3600523	5937.029526	6.556366	3.773569
35	Algeria	2007	72.301	33333216	6223.367465	7.522877	3.794025
47	Angola	2007	42.731	12420476	4797.231267	7.094138	3.680991
59	Argentina	2007	75.320	40301927	12779.379640	7.605326	4.106510
...	...	...	...	...	...	...	...
1655	Vietnam	2007	74.249	85262356	2441.576404	7.930757	3.387670
1667	West Bank and Gaza	2007	73.422	4018332	3025.349798	6.604046	3.480776
1679	Yemen, Rep.	2007	62.698	22211743	2280.769906	7.346583	3.358081
1691	Zambia	2007	42.384	11746035	1271.211593	7.069891	3.104218
1703	Zimbabwe	2007	43.487	12311143	469.709298	7.090298	2.671829

142 rows × 7 columns

In the last problem set, you generated a graph that predicted life expectancy as a function of income, with information about population and region available as well.

gap

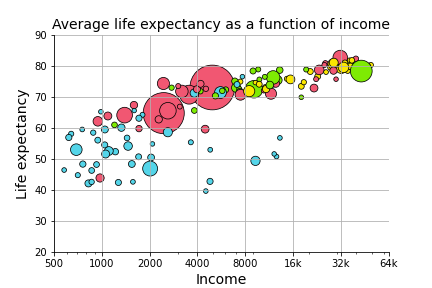
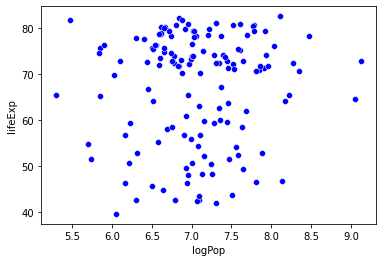
The graph suggests that life expectancy is strongly predicted by income, while population may not play such an important role.

Let’s test that here!

What that amounts to asking is:

Can we predict life expectancy using both income and population better than we could only using one of those variables?

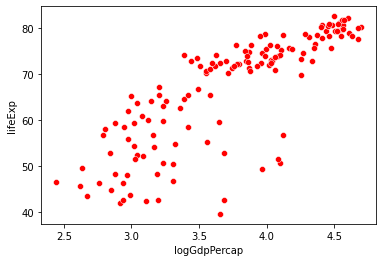
sns.scatterplot(data = gap_subset, 
                x = "logGdpPercap", # x1 
                y = "lifeExp",
                color = "r"
               )
plt.show()

sns.scatterplot(data = gap_subset, 
                x = "logPop", # x2 
                y = "lifeExp",
                color = "b"
               )
plt.show()

Multiple regression: overview¶

Multiple regression is like linear regression except that we assume our dependent variable \(y_i\) is jointly predicted by multiple independent variables \(x_1\), \(x_2\), …, \(x_n\), as in the example above.

As noted above, our simple linear regression model assumes that our data \((x_i, y_i)\) has the following form:

\(y_i = \beta_0 + \beta_1 x_i + \epsilon_i\)

With multiple regression, we now extend this model to include multiple predictors:

\(y_i = \beta_0 + \beta_1 x_{i,1} + \beta_2 x_{i,2} + \ ... \ + \beta_n x_{i,n} + \epsilon_i \)

In most cases, multiple regression once again uses the same Ordinary Least Squares (OLS) parameter estimation as simple regression. However, interpreting the parameter estimates is a little less straightforward.

How would we interpret \(\beta_0 = 1\), \(\beta_1 = 2\), \(\beta_2 = 3\)?

Multiple regression in python¶

To run our multiple regression, we can use the scikit LinearRegression class with just a few modifications to our simple regression code.

I’ve also included the statsmodels code below as well so we can look at the statistics more closely!

# scikit learn approach
x_vals = np.array(gap_subset[['logGdpPercap', 'logPop']]) # Note: this syntax is important!
x_vals = x_vals.reshape(len(gap_subset), 2)
x_vals

y_vals = np.array(gap_subset['lifeExp'])
y_vals

mod = LinearRegression().fit(X = x_vals, y = y_vals)

mod.intercept_
mod.coef_

array([16.6811828 ,  1.86827925])

# How well does our regression do?
mod.score(X = x_vals, y = y_vals)

0.6649393884784984

Using the statsmodels regression class, we can view statistical tests on our parameter fits

multiple_reg = smf.ols('lifeExp ~ logGdpPercap + logPop', data = gap_subset).fit()

# View the results
multiple_reg.summary()

OLS Regression Results
Dep. Variable:	lifeExp	R-squared:	0.665
Model:	OLS	Adj. R-squared:	0.660
Method:	Least Squares	F-statistic:	137.9
Date:	Wed, 25 May 2022	Prob (F-statistic):	9.91e-34
Time:	09:23:10	Log-Likelihood:	-477.07
No. Observations:	142	AIC:	960.1
Df Residuals:	139	BIC:	969.0
Df Model:	2
Covariance Type:	nonrobust

	coef	std err	t	P>\|t\|	[0.025	0.975]
Intercept	-8.6161	7.538	-1.143	0.255	-23.520	6.288
logGdpPercap	16.6812	1.008	16.555	0.000	14.689	18.673
logPop	1.8683	0.896	2.086	0.039	0.098	3.639

Omnibus:	34.155	Durbin-Watson:	2.170
Prob(Omnibus):	0.000	Jarque-Bera (JB):	54.987
Skew:	-1.183	Prob(JB):	1.15e-12
Kurtosis:	4.923	Cond. No.	104.

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

Lecture 14 (4/27/2022) Week 6

UCSD CSS 2