2022)¶

Announcements

Today’s lab + OH on zoom as well! See announcement from Purva
This week’s lab due Friday 5/27!
Plan for upcoming lectures
- Friday 5/27: last “official course content” lecture
- Monday 5/30: no class (holiday)
- Wednesday 6/1: class in ERC 117 for final project presentations
  - Sign up for a slot here
- Friday 6/3: special topic: APIs

Last time we covered:

Dimensionality reduction: intro to Principal Components Analysis

Today’s agenda:

Interpreting PCA results (cont’d from last time) + Evaluating PCA
- These are kind of interchangeable so we’ll mostly be presenting interpretation and evaluation measures together

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

Interpreting Principal Components Analysis¶

Review¶

On Monday, we walked through the basics of how PCA works and how to implement it with the sklearn PCA class.

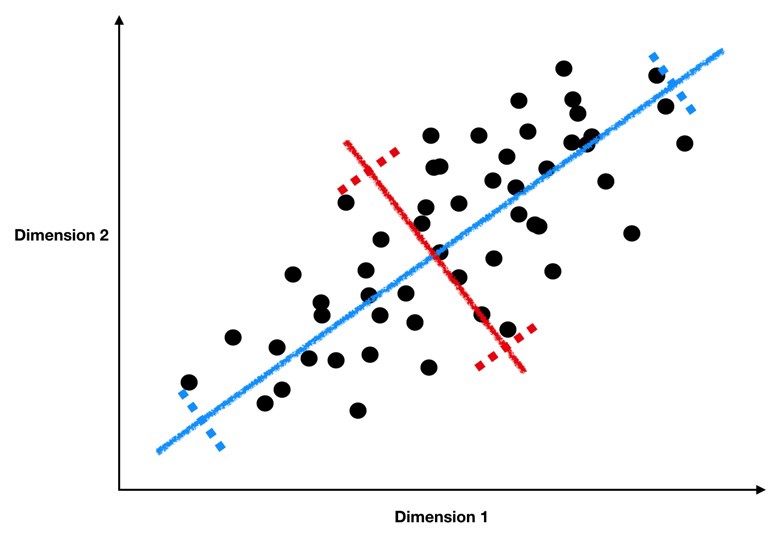
As a reminder, we’re looking for lines like the blue and red ones below, which form the principal components of our data.

pca_static

(Source)

These lines have two key properties:

They represent the axes on which our data has the highest variance (the first principal component is the highest, the second is the second highest, …)
They are orthogonal to each other, meaning they are independent as predictors of our data

Because of these properties, when we project our data onto the principal components, we can often describe most of the variance in our high-dimensional data with only a few principal component axes. In other words, they provide a high fidelity summary of what our data is doing without needing all the original dimensions.

pca

(Source)

For this reason, PCA is one of the most popular dimensionality reduction techniques in modern data science.

Today, we’re going to talk about how to interpret and evaluate our PCA resuls.

Example: low-dimensional representation of pokemon attributes¶

Today, we’ll use the pokemon dataset, which we’ve discussed in previous lectures and assignments, to create a low-dimensional encoding of pokemon attributes.

In the data below, take a look at the columns indicating each pokemon’s effectiveness (HP, Attack, Defense, Sp. Atk, Sp. Def, Speed); we need a very high-dimensional representation of each pokemon if we use all these columns to cluster or classify them!

# Read in the data
pokemon = pd.read_csv("https://raw.githubusercontent.com/erik-brockbank/css2_sp22-public/main/Datasets/Pokemon.csv")
pokemon

	#	Name	Type 1	Type 2	Total	HP	Attack	Defense	Sp. Atk	Sp. Def	Speed	Generation	Legendary
0	1	Bulbasaur	Grass	Poison	318	45	49	49	65	65	45	1	False
1	2	Ivysaur	Grass	Poison	405	60	62	63	80	80	60	1	False
2	3	Venusaur	Grass	Poison	525	80	82	83	100	100	80	1	False
3	3	VenusaurMega Venusaur	Grass	Poison	625	80	100	123	122	120	80	1	False
4	4	Charmander	Fire	NaN	309	39	52	43	60	50	65	1	False
...	...	...	...	...	...	...	...	...	...	...	...	...	...
795	719	Diancie	Rock	Fairy	600	50	100	150	100	150	50	6	True
796	719	DiancieMega Diancie	Rock	Fairy	700	50	160	110	160	110	110	6	True
797	720	HoopaHoopa Confined	Psychic	Ghost	600	80	110	60	150	130	70	6	True
798	720	HoopaHoopa Unbound	Psychic	Dark	680	80	160	60	170	130	80	6	True
799	721	Volcanion	Fire	Water	600	80	110	120	130	90	70	6	True

800 rows × 13 columns

Let’s find the principal components of these pokemon behavior attributes to create a lower-dimensional representation:

from sklearn.decomposition import PCA

# Use these columns as the basis for PCA
cols = ['HP', 'Attack', 'Defense', 'Sp. Atk', 'Sp. Def', 'Speed']

# Fit the PCA class to our data
pca = PCA(random_state = 1).fit(pokemon.loc[:, cols])
pca

PCA(random_state=1)

How effective is PCA here?

Look at the explained variance ratio to see how many principal components we need to account for a large amount of the variance in our data

Proportion of explained variance: how well do our principal components summarize the data?¶

A good first step after running PCA is to see how well each successive component accounts for variance in our original data. Remember, the principal components are identified in order of how much of the variance in the data they can explain.

A good PCA result will show that you can account for a large percentage of the variance in the underlying data with much fewer dimensions.

sns.pointplot(x = np.arange(1, pca.n_components_ + 1), y = pca.explained_variance_ratio_)
plt.xlabel("Principal component")
plt.ylabel("Proportion of additional variance explained")
plt.show()

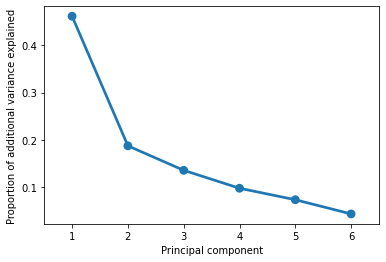
The plot above suggests that we can explain 70-80% of variance in our (6-dimensional) data with just 2-3 dimensions. In other words, a lof the general pattern of our data is captured by a couple key axes.

We can confirm this by adding up the actual values from the graph above:

pca.explained_variance_ratio_[0] + pca.explained_variance_ratio_[1]

0.6484827653819596

So what are these axes?

Remember that a “principal component” is just a line through our data, expressed via weights on each of the existing dimensions that are a lot like regression coefficients. Like regression coefficients, these weights tell us about the pattern in our original variables that each principal component is capturing.

Principal component weights: what are the key “axes” along which our data varies?¶

Below, we’ll plot the weights applied to each of our original dimensions to create the principal components. Ideally, these should give us some indication of the smaller number of “axes” that our data varies along.

sns.barplot(x = pca.components_[0], y = cols)
plt.title("Component 1")
plt.show()

sns.barplot(x = pca.components_[1], y = cols)
plt.title("Component 2")
plt.show()

sns.barplot(x = pca.components_[2], y = cols)
plt.title("Component 3")
plt.show()

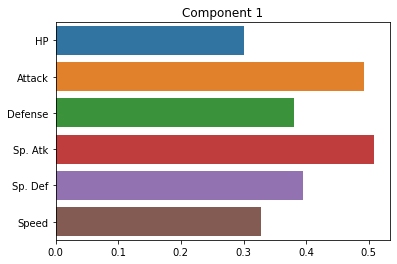
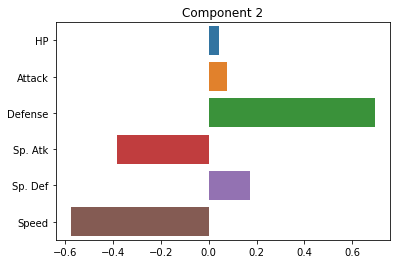
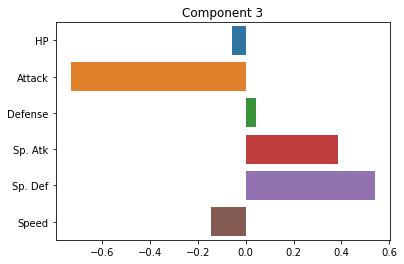
How do we interpret these plots? What does each one mean?

Ideally, should have some interpretation in terms of more abstract patterns in the data.

Note: PCA can sometimes present challenges in interpreting the principal components. In some cases, they may index really clear aspects of the data. In other cases, they may be more ambiguous. For this reason, it’s best to have a grasp of the domain of the data when interpreting PCA. Like unsupervised clustering we talked about last week, it requires more subjective interpretation than our supervised methods.

Transforming data onto principal components: how well do they summarize our data?¶

Since our principal components are new orthogonal lines drawn through our data, we can plot the value that each of our original data points takes on when projected onto these lines.

If the first 2-3 principal components describe our data well, we should see it line up in a fairly orderly way along these axes.

Our first step is to transform our original data into a position on each of the principal components that our PCA identified:

pokemon_transform = pca.transform(X = pokemon.loc[:, cols])
pokemon_transform = pd.DataFrame(pokemon_transform, columns = ['Component ' + str(i) for i in np.arange(1, pca.n_components_ + 1)])

pokemon_transform

	Component 1	Component 2	Component 3	Component 4	Component 5	Component 6
0	-45.860728	-5.384432	18.925550	-0.988558	-12.398527	10.548700
1	-11.152937	-5.805620	20.848717	0.269407	-5.800877	7.175004
2	36.946009	-5.236130	21.520463	1.531646	2.445413	3.159865
3	80.128413	18.995343	29.313909	-11.228419	-8.684840	0.214346
4	-50.385905	-21.792797	3.921880	-12.581893	-7.357519	3.041302
...	...	...	...	...	...	...
795	72.196952	67.431919	44.284620	-34.857821	-10.971975	26.977909
796	120.944879	-20.303238	-8.390285	-38.395104	-44.341807	21.930314
797	75.999885	-27.270786	37.017466	19.106076	-28.247968	39.369910
798	114.096713	-36.870567	6.750875	17.902908	-45.622767	54.767251
799	72.883550	15.152616	10.180516	-3.206397	-32.026195	-11.208742

800 rows × 6 columns

The dataframe above shows us the values of each row of our original data projected onto the principal components.

In other words, instead of each Pokemon’s values in \(x_1\), \(x_2\), …, \(x_n\), it shows us each pokemon’s new value on \(pc_1\), \(pc_2\), …, \(pc_n\).

Let’s add these to our original dataframe so we can do interesting comparisons:

pokemon = pd.concat([pokemon, pokemon_transform], axis = 1)
pokemon

	#	Name	Type 1	Type 2	Total	HP	Attack	Defense	Sp. Atk	Sp. Def	Speed	Generation	Legendary	Component 1	Component 2	Component 3	Component 4	Component 5	Component 6
0	1	Bulbasaur	Grass	Poison	318	45	49	49	65	65	45	1	False	-45.860728	-5.384432	18.925550	-0.988558	-12.398527	10.548700
1	2	Ivysaur	Grass	Poison	405	60	62	63	80	80	60	1	False	-11.152937	-5.805620	20.848717	0.269407	-5.800877	7.175004
2	3	Venusaur	Grass	Poison	525	80	82	83	100	100	80	1	False	36.946009	-5.236130	21.520463	1.531646	2.445413	3.159865
3	3	VenusaurMega Venusaur	Grass	Poison	625	80	100	123	122	120	80	1	False	80.128413	18.995343	29.313909	-11.228419	-8.684840	0.214346
4	4	Charmander	Fire	NaN	309	39	52	43	60	50	65	1	False	-50.385905	-21.792797	3.921880	-12.581893	-7.357519	3.041302
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
795	719	Diancie	Rock	Fairy	600	50	100	150	100	150	50	6	True	72.196952	67.431919	44.284620	-34.857821	-10.971975	26.977909
796	719	DiancieMega Diancie	Rock	Fairy	700	50	160	110	160	110	110	6	True	120.944879	-20.303238	-8.390285	-38.395104	-44.341807	21.930314
797	720	HoopaHoopa Confined	Psychic	Ghost	600	80	110	60	150	130	70	6	True	75.999885	-27.270786	37.017466	19.106076	-28.247968	39.369910
798	720	HoopaHoopa Unbound	Psychic	Dark	680	80	160	60	170	130	80	6	True	114.096713	-36.870567	6.750875	17.902908	-45.622767	54.767251
799	721	Volcanion	Fire	Water	600	80	110	120	130	90	70	6	True	72.883550	15.152616	10.180516	-3.206397	-32.026195	-11.208742

800 rows × 19 columns

Now, let’s get a sense of how well our first couple principal components summarize our data by plotting the data projected onto these components:

In other words, we plot each of our data points but instead of plotting them on our original axes, we plot them on the new principal component axes:

sns.scatterplot(data = pokemon, x = "Component 1", y = "Component 2", alpha = 0.5)
plt.show()

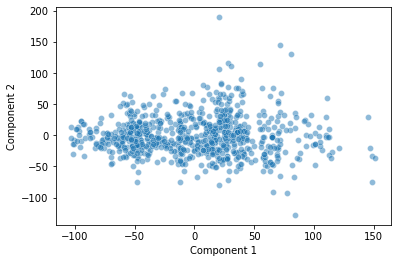
How should we interpret this plot? What does it show?

PC1 does a really nice job capturing variance in our data long its axis. PC2 as well.

Applying Principal Components: can we understand our data better by looking at the primary axes it varies along?¶

In the plot above, there seemed to be an intriguing discontinuity in our data along the first two principal components.

One way to evaluate PCA is to see how well it affords the analyses we want to do with our high-dimensional data, like classification and clustering.

sns.scatterplot(data = pokemon, x = "Component 1", y = "Component 2", alpha = 0.5)
plt.axvline(x = 50, c = "r", ls = "--")
plt.show()

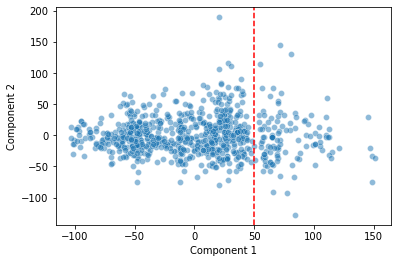
Is the discontinuity in our first principal component telling us something useful about how our data is arranged in high-dimensional space?

One way we can approach this question is by applying a clustering algorithm to our data, but now we’ll cluster along the principal components rather than the original data points.

This tells us how our low-dimensional data representation can be clustered.

Does a Gaussian Mixture Model cluster according to the discontinuity we detected above?

from sklearn.mixture import GaussianMixture

# Fit a GMM with 4 clusters
gm = GaussianMixture(n_components = 4, random_state = 1)

# Then, generate labels for each of our data points based on these clusters
preds = gm.fit_predict(X = pokemon.loc[:, ('Component 1', 'Component 2')])

# Finally, let's add these labels to our original dataframe
pokemon['pca_lab'] = preds

pokemon

	#	Name	Type 1	Type 2	Total	HP	Attack	Defense	Sp. Atk	Sp. Def	Speed	Generation	Legendary	Component 1	Component 2	Component 3	Component 4	Component 5	Component 6	pca_lab
0	1	Bulbasaur	Grass	Poison	318	45	49	49	65	65	45	1	False	-45.860728	-5.384432	18.925550	-0.988558	-12.398527	10.548700	1
1	2	Ivysaur	Grass	Poison	405	60	62	63	80	80	60	1	False	-11.152937	-5.805620	20.848717	0.269407	-5.800877	7.175004	3
2	3	Venusaur	Grass	Poison	525	80	82	83	100	100	80	1	False	36.946009	-5.236130	21.520463	1.531646	2.445413	3.159865	3
3	3	VenusaurMega Venusaur	Grass	Poison	625	80	100	123	122	120	80	1	False	80.128413	18.995343	29.313909	-11.228419	-8.684840	0.214346	0
4	4	Charmander	Fire	NaN	309	39	52	43	60	50	65	1	False	-50.385905	-21.792797	3.921880	-12.581893	-7.357519	3.041302	1
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
795	719	Diancie	Rock	Fairy	600	50	100	150	100	150	50	6	True	72.196952	67.431919	44.284620	-34.857821	-10.971975	26.977909	2
796	719	DiancieMega Diancie	Rock	Fairy	700	50	160	110	160	110	110	6	True	120.944879	-20.303238	-8.390285	-38.395104	-44.341807	21.930314	0
797	720	HoopaHoopa Confined	Psychic	Ghost	600	80	110	60	150	130	70	6	True	75.999885	-27.270786	37.017466	19.106076	-28.247968	39.369910	0
798	720	HoopaHoopa Unbound	Psychic	Dark	680	80	160	60	170	130	80	6	True	114.096713	-36.870567	6.750875	17.902908	-45.622767	54.767251	0
799	721	Volcanion	Fire	Water	600	80	110	120	130	90	70	6	True	72.883550	15.152616	10.180516	-3.206397	-32.026195	-11.208742	0

800 rows × 20 columns

Now, let’s see how well the clustering above did with our data arranged along the first two principal components:

sns.scatterplot(data = pokemon, 
                x = "Component 1", 
                y = "Component 2", 
                hue = "pca_lab",
                alpha = 0.5)
plt.show()

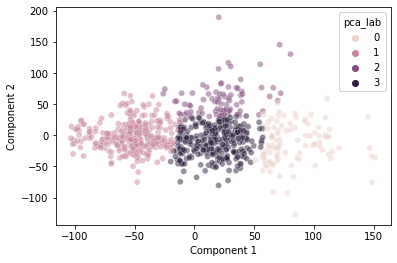
This seems to do a decently good job clustering our data.

Interestingly, it does somewhat capture the discontinuity we observed at \(pc_1 = 50\), though not perfectly.

As an aside, we can show that 4 clusters is a pretty good choice using the “elbow method” with the GMM’s “Akaike Information Criterion” below:

clusters = np.arange(1, 11)
scores = []

for k in clusters:
    scores.append(GaussianMixture(n_components = k, random_state = 1).fit(
            X = pokemon.loc[:, ('Component 1', 'Component 2')]).aic(
            X = pokemon.loc[:, ('Component 1', 'Component 2')]))
scores
    
sns.lineplot(x = clusters, y = scores)

<AxesSubplot:>

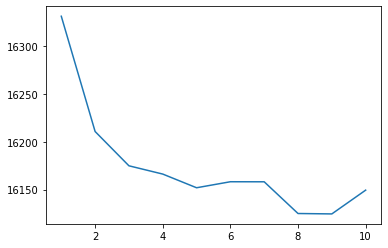
So what’s happening at that discontinuity in our first principal component?

Is there anything interpretable in our data that the PCA identified?

Note, there’s nothing guaranteeing that this will be the case, but here, it looks like this discontinuity may in part reflect whether a pokemon is “Legendary” or not!

sns.scatterplot(data = pokemon, 
                x = "Component 1", 
                y = "Component 2", 
                hue = "Legendary",
                alpha = 0.5)
plt.show()

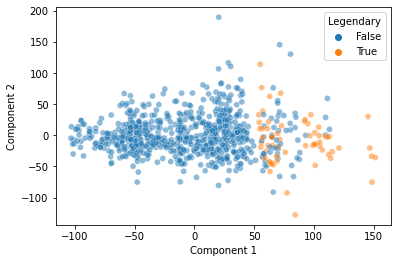
That’s pretty cool! Our Principal Components Analysis showed us a pattern in our data along the primary axes that our data varies on.

And, when we cluster based on those primary axes, we do a decent job separating out the “Legendary” pokemon based on this discontinuity:

sns.scatterplot(data = pokemon, 
                x = "Component 1", 
                y = "Component 2", 
                hue = "pca_lab",
                style = "Legendary",
                alpha = 0.5)
plt.show()

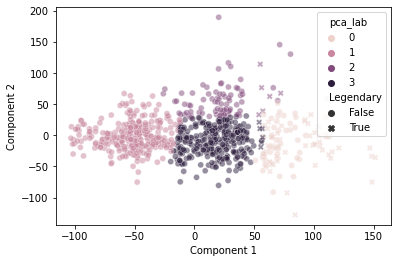
It’s not perfect, but pretty good!

Now, if you’re skeptical of the above, you might be thinking, “maybe we could have done all this without our fancy PCA and clustering based on principal components.”

When we look at our data with “Legendary” pokemon highlighted in each of the two-dimensional representations of our original data, it seems kind of unlikely that a clustering solution would easily isolate those labels…

cols.append('Legendary')
sns.pairplot(pokemon.loc[:, cols],
             hue = "Legendary",
             plot_kws = {"alpha": 0.5}
            )

<seaborn.axisgrid.PairGrid at 0x7fa38ec406a0>

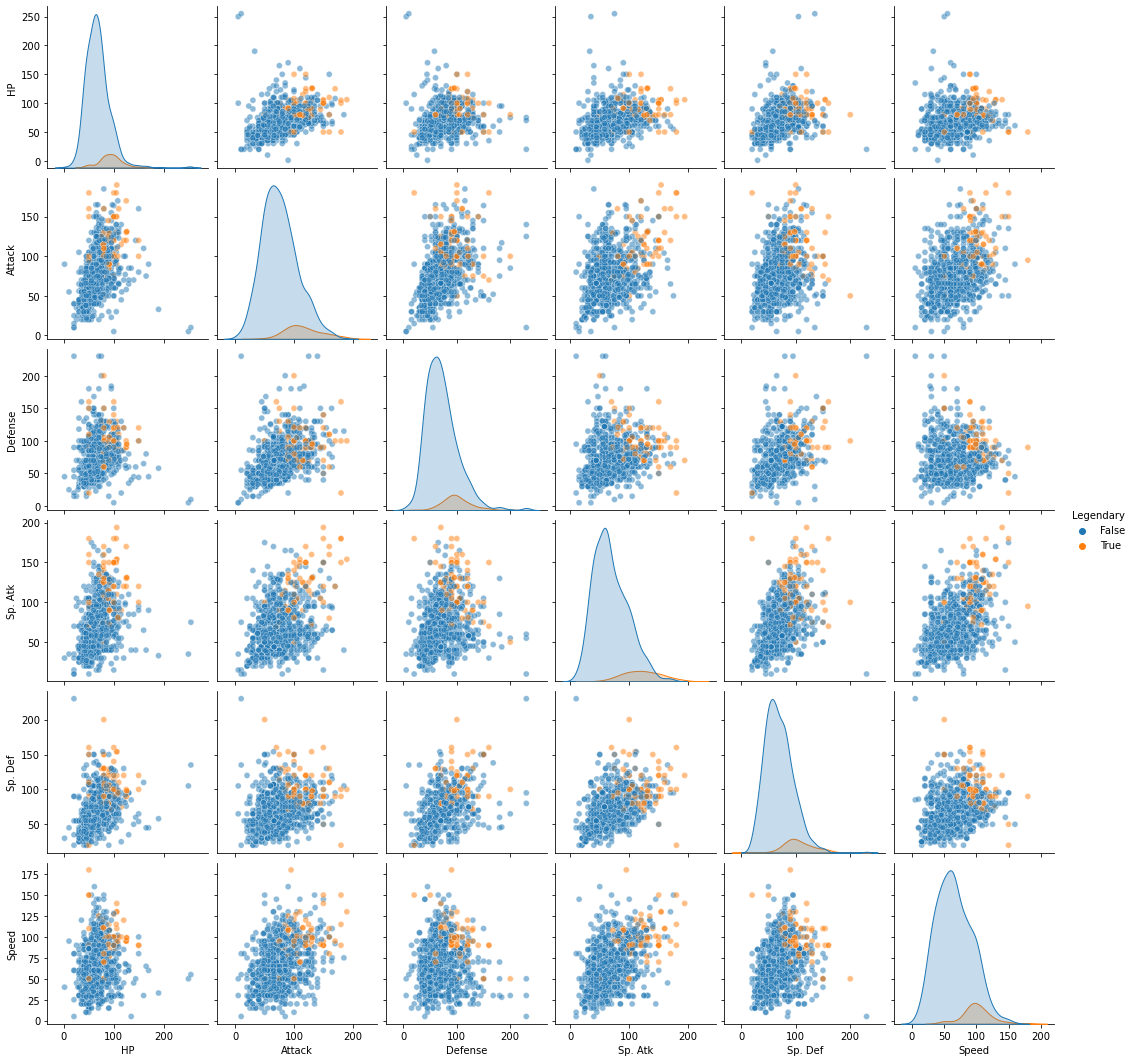
But, just for thoroughness, we can run a similar GMM with 4 clusters on the original high-dimensional data and see if we do as clean a job separating out the “Legendary” pokemon:

# Use these columns as the basis for our high-dimensional GMM
cols = ['HP', 'Attack', 'Defense', 'Sp. Atk', 'Sp. Def', 'Speed']

# Then, fit a GMM and assign the labels to our original data 
# we call them 'highd_lab' to differentiate from the PCA labels ('pca_lab')
pokemon['highd_lab'] = GaussianMixture(n_components = 4, random_state = 1).fit_predict(X = pokemon.loc[:, cols])
pokemon

	#	Name	Type 1	Type 2	Total	HP	Attack	Defense	Sp. Atk	Sp. Def	...	Generation	Legendary	Component 1	Component 2	Component 3	Component 4	Component 5	Component 6	pca_lab	highd_lab
0	1	Bulbasaur	Grass	Poison	318	45	49	49	65	65	...	1	False	-45.860728	-5.384432	18.925550	-0.988558	-12.398527	10.548700	1	1
1	2	Ivysaur	Grass	Poison	405	60	62	63	80	80	...	1	False	-11.152937	-5.805620	20.848717	0.269407	-5.800877	7.175004	3	1
2	3	Venusaur	Grass	Poison	525	80	82	83	100	100	...	1	False	36.946009	-5.236130	21.520463	1.531646	2.445413	3.159865	3	2
3	3	VenusaurMega Venusaur	Grass	Poison	625	80	100	123	122	120	...	1	False	80.128413	18.995343	29.313909	-11.228419	-8.684840	0.214346	0	3
4	4	Charmander	Fire	NaN	309	39	52	43	60	50	...	1	False	-50.385905	-21.792797	3.921880	-12.581893	-7.357519	3.041302	1	1
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
795	719	Diancie	Rock	Fairy	600	50	100	150	100	150	...	6	True	72.196952	67.431919	44.284620	-34.857821	-10.971975	26.977909	2	3
796	719	DiancieMega Diancie	Rock	Fairy	700	50	160	110	160	110	...	6	True	120.944879	-20.303238	-8.390285	-38.395104	-44.341807	21.930314	0	3
797	720	HoopaHoopa Confined	Psychic	Ghost	600	80	110	60	150	130	...	6	True	75.999885	-27.270786	37.017466	19.106076	-28.247968	39.369910	0	3
798	720	HoopaHoopa Unbound	Psychic	Dark	680	80	160	60	170	130	...	6	True	114.096713	-36.870567	6.750875	17.902908	-45.622767	54.767251	0	3
799	721	Volcanion	Fire	Water	600	80	110	120	130	90	...	6	True	72.883550	15.152616	10.180516	-3.206397	-32.026195	-11.208742	0	3

800 rows × 21 columns

How did we do here? Did these clusters also identify our “Legendary” pokemon?

One drawback of doing the high-dimensional clustering is that it’s not easy to visualize our data in this many dimensions!

Instead, we can resort to a summary based on counting the percent of “Legendary” pokemon assigned to each of our high dimensional clusters:

highd_summary = pokemon.groupby("highd_lab").agg(
    Legendary = ("Legendary", "sum"),
).reset_index()

highd_summary['Legendary_pct'] = highd_summary['Legendary'] / np.sum(highd_summary['Legendary'])
highd_summary

	highd_lab	Legendary	Legendary_pct
0	0	4	0.061538
1	1	0	0.000000
2	2	33	0.507692
3	3	28	0.430769

We did… not great. We have about 23% of our “Legendary” pokemon in one cluster, 58% in another, and 19% in a third.

How does this compare to our PCA-based clusters above, using only the first two principal components?

lowd_summary = pokemon.groupby("pca_lab").agg(
    Legendary = ("Legendary", "sum"),
).reset_index()

lowd_summary['Legendary_pct'] = lowd_summary['Legendary'] / np.sum(lowd_summary['Legendary'])
lowd_summary

	pca_lab	Legendary	Legendary_pct
0	0	53	0.815385
1	1	0	0.000000
2	2	6	0.092308
3	3	6	0.092308

With PCA and only two dimensions, we put 83% of our “Legendary” pokemon into a single cluster and less than 10% in the others. This is much better!

What’s the point of all this?

When we take our high-dimensional data and use a dimensionality reduction technique like PCA to identify the primary axes that our data varies on, this can actually help us understand our data better than in its original form.

Here, for example, we saw that the primary axis along which our data varies does a pretty good job of separating out “Legendary” pokemon from the others. Clustering algorithms based on just the first two principal components do a better job isolating these pokemon than the same algorithms applied to our original data!

Evaluating PCA along individual dimensions¶

cols = ['HP', 'Attack', 'Defense', 'Sp. Atk', 'Sp. Def', 'Speed']

pokemon_subset = pokemon.loc[:, cols]

# Fit the PCA class to our data with just two principal components
pca2 = PCA(n_components = 2).fit(pokemon_subset)

# Transform our data onto these two principal components
pca2_vals = pd.DataFrame(pca2.transform(pokemon.loc[:, cols]), columns = ["PC1", "PC2"])
pca2_vals

# Add the transformed data to our dataframe
pokemon_subset = pd.concat([pokemon_subset, pca2_vals], axis = 1)
pokemon_subset

# Run the "inverse transform" of our data projected onto the principal components
inv_transform = pca2.inverse_transform(pca2.transform(pokemon.loc[:, cols]))
inv_transform

# Make a dataframe of the new predictions and add it to our original dataframe for comparison
pca2_preds = pd.DataFrame(inv_transform, columns = [elem + "_pred" for elem in cols])
pca2_preds

pokemon_subset = pd.concat([pokemon_subset, pca2_preds], axis = 1)
pokemon_subset

	HP	Attack	Defense	Sp. Atk	Sp. Def	Speed	PC1	PC2	HP_pred	Attack_pred	Defense_pred	Sp. Atk_pred	Sp. Def_pred	Speed_pred
0	45	49	49	65	65	45	-45.860728	-5.384432	55.236205	55.984724	52.642982	51.541692	52.880090	56.370858
1	60	62	63	80	80	60	-11.152937	-5.805620	65.658802	73.059669	65.561149	69.368731	66.494554	67.972058
2	80	82	83	100	100	80	36.946009	-5.236130	80.151381	96.810835	84.265187	93.631871	85.562359	83.384973
3	80	100	123	122	120	80	80.128413	18.995343	94.163805	119.949881	117.548003	106.322678	106.805912	83.557711
4	39	52	43	60	50	65	-50.385905	-21.792797	53.182394	52.498326	39.513188	55.527978	48.242175	64.342455
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
795	50	100	150	100	150	50	72.196952	67.431919	93.822481	119.748098	148.202887	83.719427	112.100828	53.058732
796	50	160	110	160	110	110	120.944879	-20.303238	104.782914	137.059880	105.763167	142.161063	116.068896	119.554513
797	80	110	60	150	130	70	75.999885	-27.270786	90.969004	114.373532	83.811600	121.955673	97.132328	108.859557
798	80	160	60	170	130	80	114.096713	-36.870567	102.023620	132.416331	91.638649	145.025926	110.487221	126.857459
799	80	110	120	130	90	70	72.883550	15.152616	91.822291	116.084807	112.118834	104.108145	103.280528	83.400454

800 rows × 14 columns

# What is the difference between our original values and our "predicted" values?
pokemon_subset[cols] - pca2.inverse_transform(pca2.transform(pokemon_subset[cols]))

	HP	Attack	Defense	Sp. Atk	Sp. Def	Speed
0	-10.236205	-6.984724	-3.642982	13.458308	12.119910	-11.370858
1	-5.658802	-11.059669	-2.561149	10.631269	13.505446	-7.972058
2	-0.151381	-14.810835	-1.265187	6.368129	14.437641	-3.384973
3	-14.163805	-19.949881	5.451997	15.677322	13.194088	-3.557711
4	-14.182394	-0.498326	3.486812	4.472022	1.757825	0.657545
...	...	...	...	...	...	...
795	-43.822481	-19.748098	1.797113	16.280573	37.899172	-3.058732
796	-54.782914	22.940120	4.236833	17.838937	-6.068896	-9.554513
797	-10.969004	-4.373532	-23.811600	28.044327	32.867672	-38.859557
798	-22.023620	27.583669	-31.638649	24.974074	19.512779	-46.857459
799	-11.822291	-6.084807	7.881166	25.891855	-13.280528	-13.400454

800 rows × 6 columns

# What is the mean of these differences squared in each column?
((pokemon_subset[cols] - pca2.inverse_transform(pca2.transform(pokemon_subset[cols])))**2).mean()

HP         425.808290
Attack     445.921493
Defense    127.285682
Sp. Atk    281.520945
Sp. Def    358.746080
Speed      245.169533
dtype: float64

What does this tell us?

The mean squared error for each of our columns when we project them onto the principal components gives us an indication of how much information we lose when we project our original data in high dimensions onto (in this case) just two principal components.

Now, we can calculate something kind of like \(R^2\) to see how much of the variance in each column’s individual values is accounted for by the principal component predictions.

# This is the mean total sum of squares for each column (essentially the variance)
((pokemon_subset[cols] - pokemon_subset[cols].mean())**2).mean()

HP          651.204298
Attack     1052.163748
Defense     971.195194
Sp. Atk    1069.410100
Sp. Def     773.480494
Speed       843.455494
dtype: float64

# When we divide the mean sum of squared "residuals" by the mean total sum of squares (and subtract from 1),
# this gives us an R^2 metric for our PCA broken out by each column
1 - (((pokemon_subset[cols] - pca2.inverse_transform(pca2.transform(pokemon_subset[cols])))**2).mean() / ((pokemon_subset[cols] - pokemon_subset[cols].mean())**2).mean())

HP         0.346122
Attack     0.576186
Defense    0.868939
Sp. Atk    0.736751
Sp. Def    0.536192
Speed      0.709327
dtype: float64

Lecture 25 (5/23/2022)

UCSD CSS 2